Example: Modifiable Lists

So-called modifiable lists (modlists, for short) are analygous to ordinary linked lists except that in a modifiable list, each cell stores the next cell (i.e., it's "tail") in a modifiable reference rather than in a ordinary pointer field. Concretely, the cells of a modifiable list are instances of the following struct:

typedef struct cons_cell_s {
  void* hd;      /* "head" */
  modref_t* tl;  /* "tail" */
} cons_cell_t;

When a meta program uses a modlist as an input to some core program, the modifiable references in the list allow the meta program to insert and delete list elements and propagate these changes through the core program (as usual, using slime_propagate).

Allocating and Initializing List Cells

To initialize a new list cell, we'll use an initialization function like this:

ifun cons_cell_init(cons_cell_t* cell, void* hd) {
  cell->hd = hd;
  cell->tl = modref();
}

This function initializes memory for a list cell with a given element (hd). It also creates an empty modref to hold the tail of the list. We use the return type ifun for all initialization functions, which is a special synonym for void.

Given this initialization function, we'll allocate new cons cells using the alloc primitive:

cons_cell_t* Cons(void* hd) {
  return alloc(sizeof(cons_cell_t), cons_cell_init, hd);
}

The alloc primitive takes: a size, the number of bytes to allocate; an initialization function to initialize the allocated memory; and zero or more initialization arguments, which are in turn passed to the initialization function. In the use above there is one initialization argument: the element to place in the "head" of the cons cell.

Creating a List

Now that we can allocate new cons cells, we can write a simple function that stores the elements of an array in a modlist:

void modlist_from_array(void** eltv, int eltc, modref_t* list) {
  modref_t* tl = list;
  int i;
  for(i = 0; i < eltc; i++) {
    cons_cell_t* cell = Cons(eltv[i]);
    write(tl, cell);
    tl = cell->tl;
  }
  write(tl, NULL);
}

Note this this is a meta function, not a core function. In particular, the accesses of the array are not tracked, and future changes to the array will not affect the list. Functions like this are typically used by the meta program to build an input for a from-scratch run. After this run, the meta program can change the list (by inserting or removing some elements), and propagate these changes through any core program that uses the list as an input.

Mapping a List

Now consider the following core function: it takes a modlist as an input and produces a new modlist as an output where the input list elements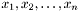 $x_1, x_2, \ldots, x_n$ are mapped to corresponding output elements 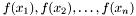$f(x_1), f(x_2),\ldots, f(x_n)$ by a given mapping function $f$

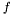. We can write this simple function both iteratively and via tail-recursion.

Iteratively

The iterative style, common to conventional C programming, uses a while loop to iterate through the cells in the input list and generate the corresponding cells of the output list:

afun modlist_map_iter(cons_cell_t* cell_in,
                      void* (*f)(void* elt),
                      modref_t* dest)
{
  while(cell_in != NULL) {
    cons_cell_t* cell_out = Cons(f(cell_in->hd));
    write(dest, cell_out);
    dest = cell_out->tl;
    cell_in = read(cell_in->tl);
  }
  write(dest, NULL);
}

via Tail-Recursion

The tail-recursive style, common to functional programming, uses a recursive call to process the "tail" of the input list and build the corresponding "tail" of the output list. Recall that core functions must be written in destination-passing style (DPS); i.e., they communicate results through modref destinations that are passed as arguments, rather than by returning results directly as return values.

afun modlist_map_rec(cons_cell_t* cell_in,
                     void* (*f)(void* elt),
                     modref_t* dest)
{
  if(cell_in == NULL)
    write(dest, NULL);
  else {
    cons_cell_t* cell_out = Cons(f(cell_in->hd));
    write(dest, cell_out);
    modlist_map_rec(read(cell_in->tl), f, cell_out->tl);
  }
}

cealc attempts to realize a recursive call with an intra-procedural jump (i.e., a "goto") whenever it appears in a so-called "tail-position", as it does in this example. As a result of this, the iterative and tail-recursive solutions we've shown here exhibit the same performance characteristics (e.g., both use a bounded amount of stack space, regardless of the length of the input list).

Splitting and Merging Lists

List-sorting algorithms like quicksort and mergesort are often implemented with simple list primitives that:

Split an input list (using some unary predicate) into two sublists.
Merge two input lists into a single output list (using some binary predicate).

For example, quicksort works by choosing a pivot element and splitting the remaining elements into two lists that contain, repsectively, the elements that are less than the pivot and the elements that are greater than the pivot. Recursively it sorts each of the two sublists, and then appends them, along with the pivot element, to create a sorted output list.

Mergesort works by splitting the input list into two sublists (of roughly equal-length), recursively sorts each sublist, and then merges these sorted lists.

We now consider the concrete implementations of these operations. We use the tail-recusion in these examples, but each can alternatively be rewritten in an iterative style, just as we did in modlist_map_iter.

Splitting a List in Two

Given a predicate f and an input list, we split the input list into two sublists. The first sublist contains all the elements for which the predicate is true, and the second sublist contains the elements for which it is false. The elements in each output list are ordered by their relative order in the input list.

afun modlist_split(cons_cell_t* cell_in,
                   int (*f)(void* elt),
                   modref_t* dest_1,
                   modref_t* dest_2)
{
  if(cell_in == NULL) {
    write(dest_1, NULL);
    write(dest_2, NULL);
  }
  else {
    cons_cell_t* cell_out = Cons(cell_in->hd);
    if(f(cell_in->hd)) {
      write(dest_1, cell_out);
      modlist_split(read(cell_in->tl), f, cell_out->tl, dest_2);
    }
    else {
      write(dest_2, cell_out);
      modlist_split(read(cell_in->tl), f, dest_1, cell_out->tl);
    }
  }
}

Merging Two Lists into One

Given a binary predicate f and two input lists, we merge the lists recursively by considering the first element of each list, call them a and b, and applying the predicate f(a,b): if true, a is added to the output list; if false, b is added. This process continues until at least one input list is empty, in which case all the remaining elements of the other input list are added to the output list.

Consider the use of this list primitive in a mergesort implementation. If the two input lists are each sorted (e.g., by recursively using mergesort) and the binary predicate reflects the ordering of the sorted elements, then the output list will contain all the input elements (from both lists) in a sorted order.

afun modlist_merge(cons_cell_t* cell_in_1,
                   cons_cell_t* cell_in_2,
                   int (*f)(void* elt_a, void* elt_b),
                   modref_t* dest)
{
  if(cell_in_1 == NULL) {
    write(dest, cell_in_2);
  }
  else if(cell_in_2 == NULL) {
    write(dest, cell_in_2);    
  }
  else {
    if(f(cell_in_1->hd, cell_in_2->hd)) {
      cons_cell_t* cell_out = Cons(cell_in_1->hd);
      write(dest, cell_out);
      modlist_merge(read(cell_in_1->tl), cell_in_2, f, cell_out->tl);
    }
    else {
      cons_cell_t* cell_out = Cons(cell_in_2->hd);
      write(dest, cell_out);
      modlist_merge(cell_in_1, read(cell_in_2->tl), f, cell_out->tl);
    }
  }
}